O que faz de uma simples questão matemática um verdadeiro desafio por mais de um século? A dissecação geométrica acaba de ganhar uma resposta definitiva, e você não vai acreditar nas implicações disso!
O enigma da dissecação geométrica
O enigma da dissecação geométrica é um desafio que fascinou matemáticos por mais de um século. A principal questão envolve dividir figuras planas, como triângulos e quadrados, em partes menores. Essas partes podem ser rearranjadas para formar uma nova figura, mas o truque é fazê-lo de maneira precisa.
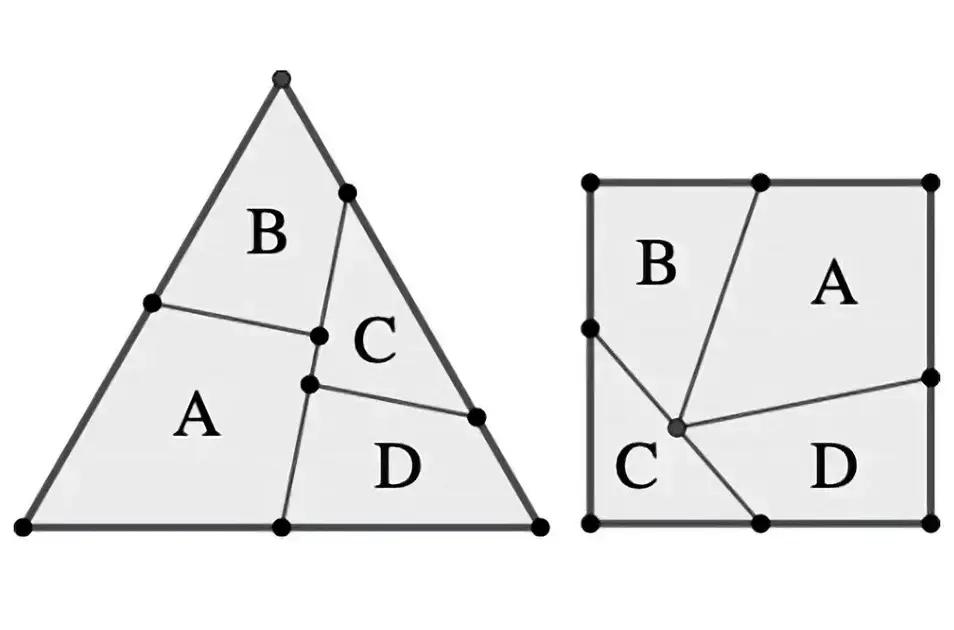
Imagine tentar transformar um triângulo em um quadrado! Isso pode parecer simples, mas requer uma compreensão profunda de formas e áreas. O matemático inglês Henry Dudeney, em 1900, propôs uma maneira de fazer isso, mas a prova dessa ideia levou 117 anos para ser completada.
Qualquer pessoa interessada em matemática pode se ver intrigada por esse enigma. Muitos tentaram e falharam, mas a curiosidade nunca morreu. Nos mais diversos círculos, o debate sobre a viabilidade e as soluções potenciais geralmente gera uma conversa animada.
Com novas técnicas e ideias, pesquisadores conseguiram resolver o quebra-cabeça de Dudeney, mostrando que e possível decompor um triângulo equilátero em um quadrado. Essa descoberta é importante porque abre portas para novas pesquisas e aplicativos práticos.
O que vem a seguir?
A resolução deste enigma poderá trazer mudanças na maneira como abordamos problemas geométricos, tanto na teoria quanto na prática. A matemática é uma ciência viva, e revisitar problemas antigos pode levar a inovações futuras e a soluções criativas.
História da proposta de Dudeney
A história da proposta de Dudeney começa em 1900. Esse matemático inglês se destacou ao criar problemas intrigantes. Um deles estava relacionado à dissecação geométrica. Ele desafiou outros matemáticos a provar se era possível transformar um triângulo equilátero em um quadrado.
Dudeney acreditava que essa mudança era viável. Ele desenhou um método que dividia o triângulo em partes menores. Com essas partes, seria possível formar um quadrado perfeito. No entanto, apesar de sua proposição, a prova não foi encontrada imediatamente.
Ao longo dos anos, muitos tentaram resolver a questão. Alguns criaram formas diferentes de abordar o problema, mas nenhuma solução era definitiva. Isso fez com que o enigma se tornasse uma curiosidade popular entre matemáticos e entusiastas.
A proposta de Dudeney ficou famosa por representar a busca por soluções em matemática. O desafio permaneceu vivo nas mentes das pessoas, gerando discussões e estudos por mais de um século. Esse mistério atraiu muitos e se tornou um clássico na história da matemática.
Finalmente, em 2017, a prova foi apresentada. Pesquisadores conseguiram irem mais fundo no assunto e explicar a viabilidade de Dudeney. Isso marca um capítulo novo devido à complexidade do problema. Essa história nos lembra que a matemática é um campo sempre em evolução.
A nova prova de otimalidade
A nova prova de otimalidade é um marco na matemática moderna. Depois de 117 anos de buscas, pesquisadores finalmente encontraram uma solução completa para o desafio da dissecação geométrica. Essa solução mostra como o triângulo equilátero pode ser transformado em um quadrado de maneira precisa.
O trabalho envolveu novas técnicas e abordagens. Os matemáticos usaram diagramas de correspondência para entender melhor a relação entre as figuras. Isso ajudou a simplificar o processo e a visualizar como cada parte se encaixa.
Essas novas metodologias não só resolveram um velho enigma, mas também abriram oportunidades no campo da matemática. Agora, a compreensão de problemas geométricos está em um novo patamar. A pesquisa também mostra como é importante revisar e redescobrir conceitos antigos.
Além disso, a descoberta traz insights que podem ser aplicados em outros campos. Por exemplo, áreas como design e engenharia podem se beneficiar da melhor compreensão de formas e como elas interagem. A matemática continua a surpreender e evoluir, trazendo soluções criativas a desafios clássicos.
Essa nova prova não é apenas um triunfo acadêmico. Também reacende o fascínio por desafios matemáticos e a exploração de ideias inovadoras. Isso inspira novas gerações a se interessarem por matemática e a buscarem novas soluções.
Abordagem inovadora com diagramas de correspondência
A abordagem inovadora com diagramas de correspondência é fundamental para entender a dissecação geométrica. Esses diagramas ajudam a visualizar como as diferentes partes de uma figura podem se encaixar. Eles transformam problemas complexos em imagens mais simples.
Na prática, essa técnica envolve desenhar diagramas que mostram a relação entre as formas. Por exemplo, ao tentar transformar um triângulo em um quadrado, é possível ver claramente como as partes do triângulo se associam às partes do quadrado.
Usar diagramas de correspondência facilita a compreensão dos passos necessários. Isso torna o processo de solução mais acessível a diferentes pessoas. Mesmo aqueles que não têm formação avançada em matemática podem entender as ideias.
Além disso, essa abordagem é útil em muitos campos. Arquitetos e engenheiros, por exemplo, podem aplicar esses conceitos para projetar estruturas. Isso mostra como a matemática e a criatividade podem andar juntas.
A simplicidade dos diagramas ajuda a despertar o interesse em matemática. Quando as pessoas conseguem ver como as formas se conectam, elas se sentem mais motivadas a aprender. Essa conexão visual é poderosa e transforma a forma como encaramos os desafios geométricos.
Implicações na matemática e design
As implicações na matemática e design são vastas e fascinantes. A recente solução para a dissecação geométrica não é apenas um triunfo acadêmico. Ela tem impactos que se estendem para várias áreas criativas.
No design, por exemplo, entender como as formas se relacionam pode levar a criações mais inovadoras. Designers gráficos e de produtos utilizam princípios geométricos para criar composições atraentes e funcionais. Saber como decompor e reorganizar figuras ajuda a desenvolver novos conceitos.
Além disso, na arquitetura, as técnicas de dissecação geométrica são úteis. Arquitetos frequentemente trabalham com formas complexas. Compreender como transformar e adaptar essas formas pode gerar estruturas mais eficientes e estéticas.
A matemática por trás dessa recente descoberta também ajuda em áreas como a arte. Artistas podem usar os princípios de correspondência de formas para criar obras mais harmoniosas. Isso leva a discussões sobre como a matemática pode influenciar a criatividade.
Com essa nova abordagem, estamos vendo a matemática se tornar uma ferramenta cada vez mais relevante em processos criativos. Os profissionais podem explorar novas possibilidades, combinando raciocínio lógico e imaginação. Isso mostra o verdadeiro poder da matemática e seu impacto em nossas vidas diárias.
Aplicações práticas da pesquisa
As aplicações práticas da pesquisa em dissecação geométrica são diversas e impactantes. A nova solução não é apenas teórica; ela pode ser aplicada em várias áreas. Por exemplo, na educação, professores podem usar esses conceitos para ensinar geometria de forma prática.
Estudantes podem aprender melhor quando veem como as formas se transformam. Usar exemplos reais ajuda a tornar a matemática mais interessante e acessível. Essa abordagem torna a aprendizagem divertida e instigante.
Além da educação, a dissecação geométrica tem uso em engenharia. Profissionais podem aplicar esses princípios em design de estruturas, otimizando espaço e materiais. Isso se traduz em construções mais eficientes e sustentáveis.
No campo da arte, artistas podem incorporar essas ideias em suas obras. Eles podem criar peças inspiradas na geometria, resultando em trabalhos que combinam beleza e matemática. Essa fusão pode gerar novas correntes artísticas.
Na tecnologia, desenvolvedores de software podem usar esses conceitos para criar algoritmos melhores. Isso pode ter um impacto significativo em áreas como gráficos computacionais e animações. Assim, a matemática mostra sua versatilidade em conectar diferentes disciplinas.
O futuro da pesquisa em dissecação geométrica
O futuro da pesquisa em dissecação geométrica promete ser brilhante e cheio de inovações. Com a recente solução encontrada, muitos matemáticos estão empolgados. Eles veem novas oportunidades para explorar conceitos antigos de maneiras frescas.
A matemática está sempre evoluindo. Novas abordagens e tecnologias ajudam na compreensão de problemas complexos. Por exemplo, o uso de software avançado pode facilitar a visualização de dissecações. Isso torna o aprendizado mais acessível a todos.
Além disso, novas descobertas podem gerar colaborações em diferentes disciplinas. Arquitetos, designers e engenheiros podem trabalhar juntos, aplicando ideias geométricas em seus projetos. A interdisciplinaridade é fundamental para impulsionar a criatividade e inovação.
Com mais pesquisas, podemos também ver aplicações práticas em áreas diversas. Isso inclui educação, onde ferramentas digitais podem tornar o ensino de geometria mais interativo. Estudantes podem aprender a dissecar figuras de forma prática e envolvente.
Por fim, a pesquisa em dissecação geométrica pode influenciar novas áreas, como a inteligência artificial. Algoritmos que utilizam princípios geométricos podem melhorar a eficiência em diversas aplicações tecnológicas. Isso mostra que a matemática sempre terá um papel importante no avanço da sociedade.
Fonte: Techno-Science.net